quinta-feira, 19 de março de 2015
Aula 6: Lei de Formação da Função Através de Enunciados.
Lei de Formação da Função Através de Enunciados.
Definimos como Lei de Formação uma maneira intuitiva de associar o valor de x a um único valor de y ou f(x) através de uma expressão algébrica. Com isso, podemos escrever uma função matemática.Nessa aula queremos que você desenvolva essa intuição e aprenda a escrever a lei de formação da função através de enunciados.
Veja os exemplos abaixo:
Exemplo 1:
Uma empresa que vende calçados paga os funcionários da seguinte forma: um salário fixo de R$ 500,00, mais R$ 2,00 por par de calçados vendidos. Quanto vai receber o funcionário que vender 10 calçados?
Para saber qual será o valor do salário de seu funcionário, a empresa faz o seguinte cálculo: 10 calçados = R$ 20,00, mais o salário fixo de R$ 500,00 é igual a R$ 520,00. Se forem vendidos 10 calçados, o funcionário receberá R$ 520,00.
Exemplo 2:
A tarifa de táxi no Rio de Janeiro é formada por: R$ 3,50 a bandeirada, mais R$ 1,70 por km rodado. Então, determine:
a) Qual é a lei de formação que define qualquer corrida de táxi no Rio de janeiro?
Podemos obter a lei de formação deste exemplo de forma similar ao exemplo 1. Neste caso a lei de formação será: Y = 3,5 + 1,7x, onde y é o valor total a pagar, e x é a quantidade de quilômetros rodados.
b) Se uma pessoa pegou o táxi e percorreu 20 km, quanto ela pagará?
Substituindo o valor de x por 20 km na lei de formação: Y = 3,5 + 1,7x, teremos:
Y = 3,5 + 1,7.(20) = 3,5 + 34 = 37,5. Logo, ele pagará R$ 37,50.
c) Se uma pessoa pagou R$ 20,50 em uma corrida, quantos km ela percorreu?
Substituindo o valor de y, que é o valor pago pela corrida, vamos ter a seguinte expressão:
Y = 3,5 + 1,7x
20,5 = 3,5 + 1,7x
1,7x = 20,5 – 3,5
1,7x = 17
X = 17/ 1,7
X = 10 km
Exemplo 3:
Um posto de gasolina da cidade do Rio de Janeiro cobra em média o preço de R$ 2,99 por litro de gasolina. Com base nessas informações, responda:
Y = 2,99x, donde y é o valor total pago pela gasolina e x é o total de litros comprados.
b) Quanto um motorista irá gastar se ele colocar em seu carro 40 litros de combustível?
Como já vimos no item anterior, temos que Y = 2,99x. Então, substituindo o valor de x, que é a quantidade de litros comprados, por 40, temos:
Y = 2,99.(40)
Y = 119,6
Esse é o valor a ser pago pela gasolina comprada.
c) Quantos litros de combustível um motorista colocou em seu carro se ele gastou apenas R$ 60,00?
Sabendo que Y = 2,99x e substituindo o valor de y, que é o preço pago pela gasolina, temos:
60 = 2,99x
X = 60/2,99
X = 20,06 litros.
Agora temos de verificar se você aprendeu. Resolva os exercícios abaixo e, em caso de dúvidas, retorne aos exemplos.
Exercícios
1- Em uma cidade, você pode alugar um carro por R$ 100,00 por dia, mais R$ 5,00 por km rodado. Dadas as informações, responda:
a) Qual é a função que descreve o aluguel do carro em um dia?
b) Qual o preço pago por uma pessoa que percorreu 12 km em um dia?
2- Uma operadora de celular cobra R$ 30,00 por mês pela assinatura, mais R$ 0,20 por minuto. Responda:
a) Qual é a função descrita a cada mês?
Na função acima, vemos uma empresa que cobra 30 reais de assinatura mais 0,20 por minuto falado.
b) Quanto gastou uma pessoa que usou 30 minutos?
c) Se um cliente pagou R$ 50,00 na conta, quantos minutos foram usados?
3- Uma locadora de filmes calcula o preço cobrado usando a seguinte fórmula: P = 3 + 1,2x, onde P é o preço a ser cobrado e x é o número de filmes alugados:
a) Qual é o preço a ser pago pelo cliente que alugou 5 filmes?
b) Quantos filmes alugou uma pessoa que pagou R$ 5,40?
4- Um posto de gasolina da rodovia está cobrando R$ 2,87 por litro de gasolina.
Responda:
a) Quanto irá pagar um motorista que colocou 30 litros de gasolina?
b) Quantos litros de gasolina o motorista colocou em seu carro se ele pagou R$ 57,00?
c) Escreva a função descrita no enunciado acima.
5- Considere um restaurante que possui um preço fixo, para todos os seus pratos, no valor de R$ 12,50, independentemente da quantidade servida. No entanto, cada porção x de sobremesa custa R$ 4,00. Das alternativas a seguir, qual melhor representa o gasto total y de um prato acompanhado de sobremesa nesse restaurante:
(A) y = 4 + 12,5x
(B) y = 12,5 + 4x
(C) y = 16,5x
(D) y = 4x + 12,5x
(E) y = 12,9x
domingo, 15 de março de 2015
sexta-feira, 13 de março de 2015
Trabalho valendo 3 PONTOS para 1003 e 1004
|
C.E. São Cristóvão
|
||||||
 |
Alunos(as)
:
|
Nº
|
||||
|
Turma:
|
Ano:
1º
|
Turno:
Tarde
|
Data:
|
|||
|
Professor:
Leandro
Ribeiro
Trabalho
|
Disciplina: Matemática
Bimestre: 1º
|
Nota:
|
||||
- Todas as questões devem ter cálculos.
- Em dupla ou individual
- Pode imprimir ou copiar
- Entregar no dia 20/03/2015
1- Dado os conjuntos A = {1, 2, 3}, B = {1, 2, 3, 5, 6}, C =
{4, 5, 6, 7} e D = {0, 1, 5, 6, 7}, classifique em verdadeiro (V) ou
falso (F).
a) A pertence B (
)
b) C não pertence A ( )
c) B pertence D
( )
d) A pertence N* ( )
2- Dado os conjuntos A = {1, 2, 3}, B = {1, 2, 3, 4, 5, 6} e
C = {4, 5, 6}, determine:
a) A – B =
b) B – C =
c) A – C =
d) B – A =
3- Dado os conjuntos A = {a, b, c, d, e, f, g }, B = { b,
d, g, h, i } e C = { e, f, m, n, }, determine:
a) A U
B =
b) A intersecção C =
c) A U
B =
d) B intersecção C =
e) ( A U B) intersecção C =
4- Considere a função para a qual A = {1, 3, 4}, B = {3, 9, 12, 15, 18} e g (x) é o triplo de x, para todo.
a) construa o diagrama de flechas da função.
b) determine D (g), CD (g) e Im (g)
c) determine g (3)
5- Calcule o valor da expressão: 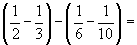
6- Calcule o valor da expressão:
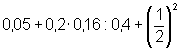
terça-feira, 10 de março de 2015
Aula 5 - Plano Cartesiano 1003 e 1004 "São Cristóvão"
Plano Cartesiano
Caro aluno, nesta atividade iremos conhecer o Plano Cartesiano. O Plano recebe este nome em homenagem ao seu criador, o matemático René Descartes. De acordo com este famoso matemático, podemos definir o plano cartesiano da seguinte forma:
O plano cartesiano é formado por duas retas
perpendiculares, uma horizontal que recebe
o nome de eixo das abscissas (eixo x) e uma
reta vertical que recebe o nome de eixo das
ordenadas (eixo y). Cada reta é numerada,
sendo o ponto de interseção dessas duas
retas chamado origem.
PLANO CARTESIANO:
A figura a seguir representa um plano cartesiano. Note que temos uma reta horizontal designada eixo das abscissas, ou eixo X, e uma reta vertical chamada eixo das ordenadas, ou eixo Y. Cada eixo é formado por números positivos e negativos, tendo o zero ao centro.
Observe:
.jpg)
Você pode observar que o Plano Cartesiano divide-se em quatro partes, que
chamaremos de quadrantes:
.jpg)
Para representar um ponto no Plano Cartesiano, iremos utilizar a seguinte representação A (x, y). Isto significa que o ponto A se localiza na direção (x, y). Observe o exemplo abaixo:

Perceba que o ponto A tem as coordenadas (- 2, 3), ou seja, x = - 2 e y = 3. Ainda sobre a localização das coordenadas no Plano Cartesiano, é importante ressaltar algumas observações:
1. O ponto (3, 4) é diferente do ponto (4, 3). Não se esqueça!! O primeiro valor se refere ao eixo x e o segundo ao eixo y.
2. O ponto (0,3) será representado exatamente sobre o ponto y = 3, no eixo y.
EXEMPLO 01:
Dado o plano cartesiano, observe os pares ordenados representados:

A (3,6) B (2,3) C (-1,2) D (-5,-3)
E (2,-4) F (3,0) G (0,5)
Exercícios
Agora que já sabemos representar as coordenadas no Plano Cartesiano, vamos exercitar nossos conhecimentos.
01. Identifique cada uma das Coordenadas de cada ponto abaixo:
A ( 10 , 5 ) B ( - 3 , 0 ) C (4 , 4 )
D ( - 3 , - 3) E ( 6 , 12 ) F ( 8 , - 10 )
G ( 0 , - 8 ) H ( 0 , 0 )
A (-2, 4) B (5, -1) C (0, 5) D (3, 0) E (-7, - 8) F (10, 0) G (0, 0) H (½, 3)
Aula 4 - Conjunto dos números irracionais 1003 e 1004 "São Cristóvão"
NÚMEROS IRRACIONAIS
Assim como existem números decimais que podem ser escritos como frações,
ou seja, o conjunto dos números racionais que acabamos de estudar, existem,
também, números que não admitem representação fracionária. Trata-se dos números
decimais não exatos que possuem representação infinita não periódica, chamado conjunto dos números irracionais i.
Vejamos alguns exemplos:
1,203040... √2 = 1,4142135... √3 = 1,7320508... PI = 3,141592...
PROPRIEDADE DOS NÚMEROS IRRACIONAIS:
Para compreendermos um pouco mais sobre o conjuntos dos números irracionais, vamos apresentar a seguir algumas propriedades muito utilizadas nos cálculos que envolvem os elementos deste conjunto. Observe:
PROPRIEDADE 1:
A soma de um número racional com um número irracional é um número irracional.
1 + √2 = 2, 4142135...
PROPRIEDADE 2:
A diferença entre um número racional e um número irracional, em qualquer ordem, é
um número irracional.
PROPRIEDADE 3:
O produto de um número racional não nulo por um número irracional é um número
irracional.
2 . √3 = 3,464101...
PROPRIEDADE 4:
O quociente de um número racional não nulo por um número irracional é um número
irracional.
12 : √6 = 4, 898979...
O NÚMERO PI (π):
O número irracional pi ( = 3,141592...) está presente em todos os lugares do nosso cotidiano. O movimento das ondas em uma praia, o aparente trajeto diário das estrelas no céu, o movimento das engrenagens e rolamentos, a propagação dos campos eletromagnéticos, entre outros fatos curiosos, estão associados às idéias de simetria circular e esférica. Ele é uma das constantes universais da Matemática.
Assim como existem números decimais que podem ser escritos como frações,
ou seja, o conjunto dos números racionais que acabamos de estudar, existem,
também, números que não admitem representação fracionária. Trata-se dos números
decimais não exatos que possuem representação infinita não periódica, chamado conjunto dos números irracionais i.
Vejamos alguns exemplos:
1,203040... √2 = 1,4142135... √3 = 1,7320508... PI = 3,141592...
PROPRIEDADE DOS NÚMEROS IRRACIONAIS:
Para compreendermos um pouco mais sobre o conjuntos dos números irracionais, vamos apresentar a seguir algumas propriedades muito utilizadas nos cálculos que envolvem os elementos deste conjunto. Observe:
PROPRIEDADE 1:
A soma de um número racional com um número irracional é um número irracional.
1 + √2 = 2, 4142135...
PROPRIEDADE 2:
A diferença entre um número racional e um número irracional, em qualquer ordem, é
um número irracional.
PROPRIEDADE 3:
O produto de um número racional não nulo por um número irracional é um número
irracional.
2 . √3 = 3,464101...
PROPRIEDADE 4:
O quociente de um número racional não nulo por um número irracional é um número
irracional.
12 : √6 = 4, 898979...
O NÚMERO PI (π):
O número irracional pi ( = 3,141592...) está presente em todos os lugares do nosso cotidiano. O movimento das ondas em uma praia, o aparente trajeto diário das estrelas no céu, o movimento das engrenagens e rolamentos, a propagação dos campos eletromagnéticos, entre outros fatos curiosos, estão associados às idéias de simetria circular e esférica. Ele é uma das constantes universais da Matemática.
Exercícios
01. Assinale a afirmação falsa.
(A) A soma de dois números naturais quaisquer é um número natural.
(B) A soma de dois números inteiros quaisquer é um número inteiro.
(C) A somo de dois números racionais quaisquer é um número racional.
(D) A soma de dois números irracionais quaisquer é um número irracional.
02. Assinale o número irracional:
(A) 0,7
(B) 0,77
(C) 0,77555...
(D) 0,71727374...
03. A fração que equivale a um número decimal não exato é:
(A) 7 / 8
(B) 4 / 25
(C) 5 / 6
(D) 33 / 40
04. Assinale a afirmação verdadeira:
(A) 0,313131... é um número natural.
(B) 5, 47 é um número inteiro.
(C) 5, 171717... é um número irracional.
(D) 4, 262626... é um número racional.
01. Assinale a afirmação falsa.
(A) A soma de dois números naturais quaisquer é um número natural.
(B) A soma de dois números inteiros quaisquer é um número inteiro.
(C) A somo de dois números racionais quaisquer é um número racional.
(D) A soma de dois números irracionais quaisquer é um número irracional.
02. Assinale o número irracional:
(A) 0,7
(B) 0,77
(C) 0,77555...
(D) 0,71727374...
03. A fração que equivale a um número decimal não exato é:
(A) 7 / 8
(B) 4 / 25
(C) 5 / 6
(D) 33 / 40
04. Assinale a afirmação verdadeira:
(A) 0,313131... é um número natural.
(B) 5, 47 é um número inteiro.
(C) 5, 171717... é um número irracional.
(D) 4, 262626... é um número racional.
Assinar:
Postagens (Atom)
